Euclidean Construction Design
This is my current obsession: the relationship between Euclidean construction and traditional design across the world.
I've created a very simple programming language for describing Euclidean constructions, and will use this to explore how some of these designs could have been (or could be) constructed. Later, I hope to also explore the use of extensions to Euclidean construction (e.g. origami) on these types of designs.
Euclidean Construction
Euclidean construction is a method for constructing figures on a canvas with just two tools: a straightedge and a compass.
Here are the production rules, which will all be demonstrated in an interactive demo below:
- The start: You start with two points [1].
- Circle, or Arc: Place the compass with one end on one point and the other end on another point and you can draw a circle. An arc can be constructed on top of a circle by having the "pen" end start at one point and end at another point.
- Line, Ray, or Line Segment: Use the straightedge to draw a line through two points, which may be cut off at one or both ends.
- Intersection: Define new points at the intersections of two figures. e.g. a line segment and a circle, or two circles, etc.
Here is an interactive demo which demonstrates most of these production rules. This demo was made using a custom programming language for describing Euclidean constructions, which will be explained in more detail later (though you can see the code that describes it with the "Code" button). Use the playback buttons to animate it.
It's interesting to note that, in this demo example, E is also the exact midpoint of A and B.
Scope of construction
These production rules are sufficient to construct many things, but are limited.
It looks like, in Euclid’s time, it was assumed that Euclidean Construction was sufficient to construct anything that was legal in Euclidean Geometry, though this was later found to not be the case.
However, it’s still rated for its simplicity, unambiguity and that it requires no system of measurement.
Design Examples
This method of construction has been well studied mathematically. It's also widely used for design, which is what I want to talk about here.
Here are a number of examples of designs that are constructible using Euclidean construction. With each example is a picture of how the design looks in the real world, followed by an interactive demo, which shows the "idealised" form of the construction and the steps that could be used to construct it. Again, the playback buttons can be used to animate backwards and forwards.
Example: London Stone Screen
I've seen Euclidean construction patterns used to design stone screens that are slotted into brick garden walls where I live in London. Here are some examples:
Four Petal

Double Tri-Cross

Example: Islamic Geometric Patterns
Islamic geometric patterns are often constructed using Euclidean construction.
The Great Mosque of Córdoba [3]
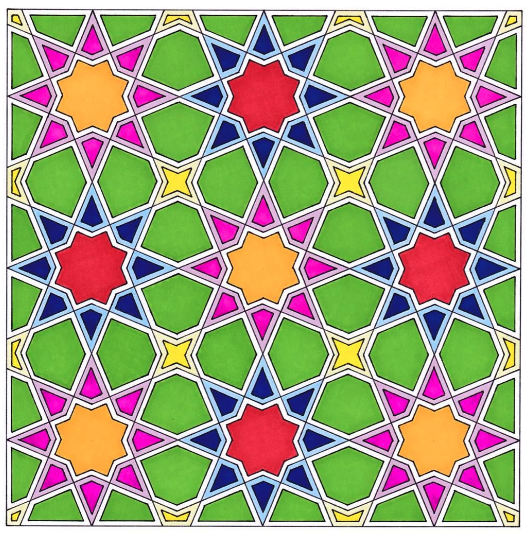
In this demo, the point names are excluded as there are so many points that they will clutter the view.
TODOs
- Christian design examples
- An editable editor, which you can use to play about with constructions yourself
Disclaimers
- Generally, you can start with some number of figures (e.g. a line, two non-overlapping circles, etc). It doesn’t have to be two points, but it seems that two points is the simplest beginning from which anything can be constructed.
- I was unfortunately not able to find a photo of the original pattern in the Great Mosque of Córdoba. This is an illustration by Ton Esink (source). The pattern for forming it was found in the book Islamic Geometric Patterns, by Eric Broug.